Julia is known to be a highly performant language, with benchmark results quite close to that of C. While that's certainly impressive, it would be even better if we can easily quantify how fast our code runs. No matter if you are a newbie or a seasoned programmer, benchmarking can help identify potential bottlenecks in your code. It can also be used to stress test your shiny new PC or laptop in my case. Luckily, there exists an excellent package BenchmarkTools.jl, which is what I will be using in the examples shown below.
Hardware
I will do a comparison of the benchmarks between two different platforms that I currently have access to:
Laptop - Dell XPS 13 Plus running Ubuntu 22.04, equipped with an Intel Core i5-1240P (12 cores, 16 threads), 16 GB LPDDR5 RAM and 1 TB NVMe SSD.
Desktop - AMD Ryzen 5 3600 (6 cores, 12 threads), 32 GB DDR4 RAM, 512 GB NVMe SSD, running on Elementary OS 7 Horus.
The RAM and SSD are likely not going to have any significant impact on the results. So, it's majorly going to be a CPU showdown - Intel vs AMD. Note that this is strictly not a one-to-one comparison since the 12th gen Intel mobile chip has a limited power budget, which means it might not be able to boost all cores to their maximum clocks. The cooling capacity of such a thin laptop is also rather limited, which could lead to thermal throttling. The desktop-class AMD processor on the other hand has a much larger power headroom to play with. Cooling is not an issue for the desktop, so all CPU cores should be able to sustain their maximum clocks when under load.
Add package
Start the Julia REPL. I am currently using version "1.8.5". Enter the pkg prompt by typing ], and then add the package:
add BenchmarkTools
Load the package
For our tests, we will also make of LinearAlgebra, which is already part of the base library (so no need to add it separately).
julia> using BenchmarkTools, LinearAlgebra
Test function
Let's create a function, which does some operations on a matrix. To summarize, we multiply the matrices, then compute the inverse, followed by tan and LU decomposition.
We can use the size of the matrix as an input argument. This will prove to be useful later since we will then be able to perform benchmark runs with increasing complexity.
julia> function do_something(size::Int64)
A = rand(size, size)
B = rand(size, size)
C = A * B
return C |> inv |> tan |> factorize
end
do_something (generic function with 1 method)
Sample run:
julia> do_something(5)
LU{Float64, Matrix{Float64}, Vector{Int64}}
L factor:
5×5 Matrix{Float64}:
1.0 0.0 0.0 0.0 0.0
0.283496 1.0 0.0 0.0 0.0
0.0128731 -0.241892 1.0 0.0 0.0
-0.148442 -0.598821 -0.950991 1.0 0.0
-0.296558 0.0199563 -0.0782248 -0.42072 1.0
U factor:
5×5 Matrix{Float64}:
1.51572 0.308015 0.235375 -0.975098 -0.42535
0.0 -1.1294 -0.103104 0.970615 0.390145
0.0 0.0 -0.395555 0.688296 0.0435477
0.0 0.0 0.0 0.893948 -0.129836
0.0 0.0 0.0 0.0 0.351661
Results will be different for every run since we haven't fixed the seed for random number generation. However, rand(size, size) will always generate a square matrix with individual entries between 0 and 1. And the sequence of operations remains unchanged once the function is defined.
Setting up the benchmark
BenchmarkTools.jl allows the use of several configuration parameters. Essentially, we want to execute the above function a certain number of times (samples) such that we have enough statistical accuracy. However, the benchmark might end up running for too long. So we would also like to limit the total time (seconds) it takes for the benchmark to run. A good rule of thumb is to start with a small sample size, and then gradually ramp it up. There's not really a downside to having a large number of sample runs. In this case, the more the merrier!
Set up the benchmark to run 50 samples within a time budget of 120 seconds. The matrix size is 100.
julia> b_N100_S50 = @benchmarkable do_something(100) seconds=120 samples=50
Test run:

That was quite fast. Let's increase the sample size to 100.
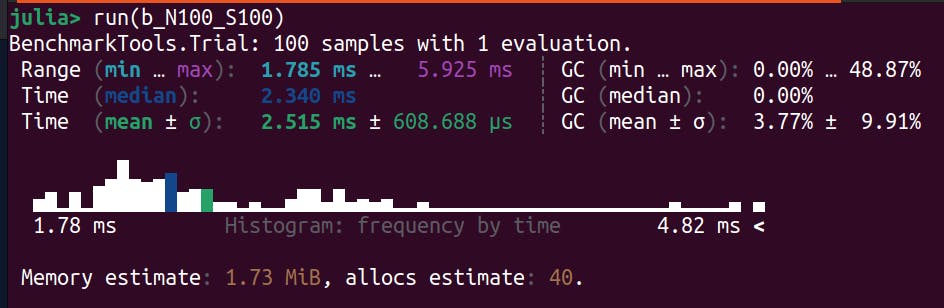
Results
Benchmark results are shown as a distribution over all the samples. In principle, code execution with a fixed input should always take the same amount of time. However, there are other sources of noise from the host machine, which usually add to the execution time. Therefore, instead of the mean, it is often argued that one should look at the minimum time to get an idea of the true baseline. In any case, we get a very nice visual representation of the time taken for all the runs including useful metrics such as the min, max, mean and median.
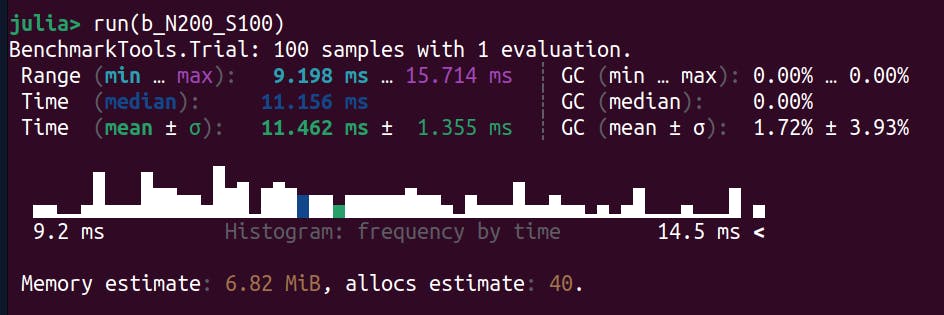
Size = 200
Intel
AMD
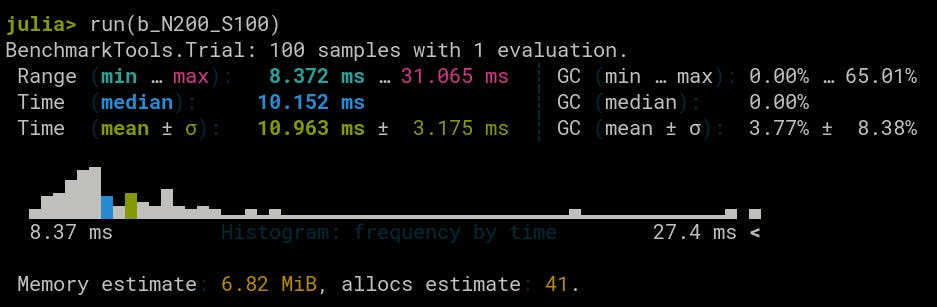
Results are comparable to each other. Let's see what happens when we increase the size of the matrix.
Size = 400
Intel
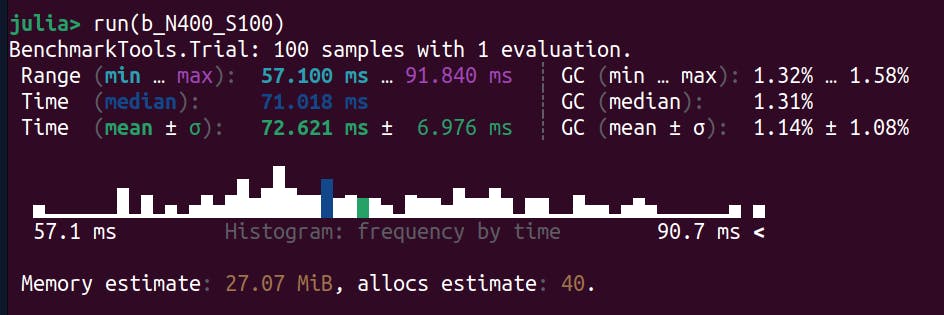
Doubling the matrix size quadruples the benchmark time.
AMD

The Ryzen CPU appears to be faster in this case.
Size = 600
Intel

Let's see if we can improve on the statistics with samples = 200.
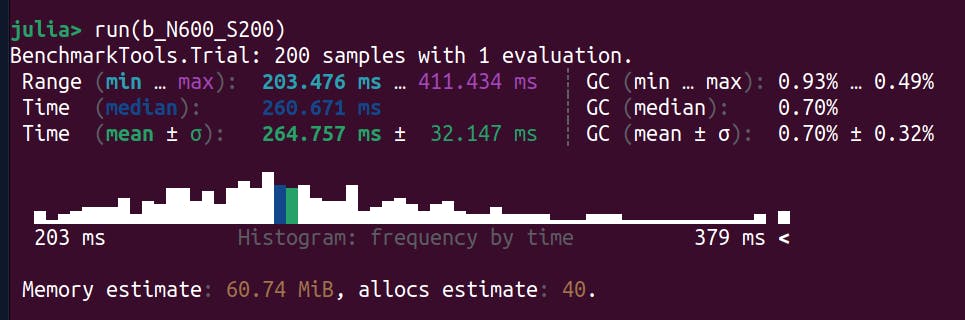
Not a huge difference in the results, so it seems 100 samples are already good enough.
AMD

The trend continues with the AMD processor being almost twice as fast.
Size = 1000
Intel
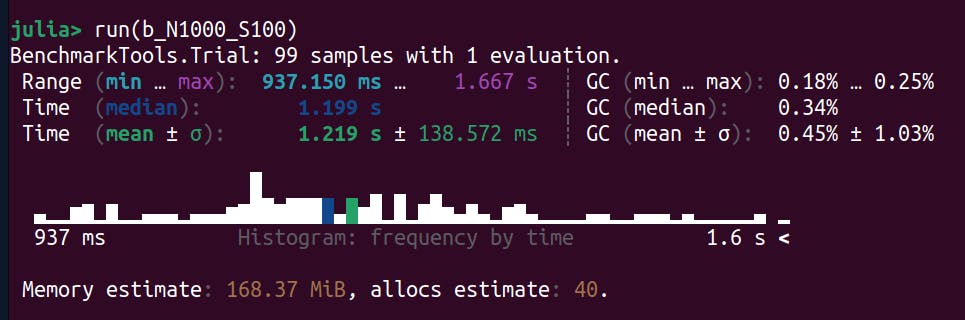
AMD

Using multiple threads
By default, Julia starts with only 1 thread. This can be checked by doing the following:
julia> Threads.nthreads()
1
However, the function is able to use 8 threads, presumably due to parallelization in the LinearAlgebra package.
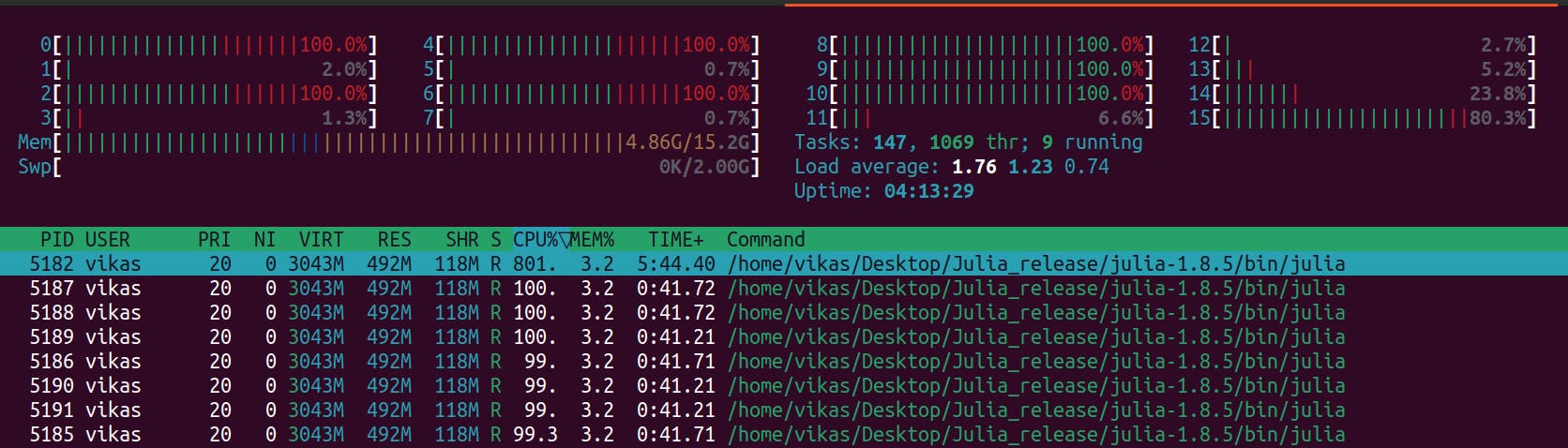
We can start Julia with multiple threads using the --threads or -t argument:
vikas@Mugetsu:~$ julia --threads 12
_
_ _ _(_)_ | Documentation: https://docs.julialang.org
(_) | (_) (_) |
_ _ _| |_ __ _ | Type "?" for help, "]?" for Pkg help.
| | | | | | |/ _` | |
| | |_| | | | (_| | | Version 1.8.5 (2023-01-08)
_/ |\__'_|_|_|\__'_| | Official https://julialang.org/ release
|__/ |
julia> Threads.nthreads()
12

Performance does not seem to be impacted by starting Julia with 12 threads. However, there are some cases where this will be very useful. I will leave that discussion for another post.
Conclusion
The desktop-class AMD processor easily outperformed the Intel CPU, which is not surprising considering that the Intel chip is limited by power and cooling. Intel chip did have more cores (and threads), but that didn't help with our benchmarks. I hope you enjoyed reading through this post and learned something new in that process. Do subscribe to this series for similar content in the future. Also, please don't forget to give it a heart and share it with other Julia enthusiasts.
